La mayoría de los fenómenos que ocurren en la naturaleza pueden ser explicados a través de cuatro interacciones que ocurren en la naturaleza. Fenómenos tales como el movimiento de los planetas, cometas y otros astros en torno al Sol, el movimiento de las cargas en un conductor que inducen a un campo magnético, las fuerzas de atracción que experimentan los electrones en torno al núcleo, la utilización de la energía de los núcleos atómicos, entre muchos otros sucesos, ocurren gracias a la acción de cuatro fuerzas.
En la naturaleza, existe la interacción de cuatro fuerzas a saber: la fuerza gravitacional, la fuerza nuclear fuerte, la fuerza electromagnética y la interacción débil.
Así mismo, según Young y Freedman (2009) “las partículas se clasifican de acuerdo con sus interacciones”. por lo tanto existen para cada interacción, un tipo de partícula específica.
Entre las características de las interacciones de las fuerzas fundamentales en la naturaleza se encuentran:
Fuerza gravitacional: Todos los cuerpos son atraídos por una fuerza que es directamente proporcional a sus masas, e inversamente proporcional al cuadrado de la distancia que los separa. La fuerza gravitacional es la causante de que los cuerpos caigan y del movimiento de los cuerpos celestes que se encuentran en el universo: planetas, satélites, estrellas, galaxias, cometas, entre otros. Su partícula mediadora es el gravitón. Posee un radio de acción infinito.

Interacción electromagnética: Es considerada la fuerza que actúa sobre las partículas con carga eléctrica. Toda carga en movimiento produce un campo magnético a su alrededor y es de naturaleza atractiva o repulsiva, dependiendo de las cargas. La partícula mediadora es el fotón. Al igual que la interacción gravitacional, posee un radio de acción infinito.

Interacción nuclear fuerte: Es la interacción más fuerte que existe y permite mantener los nucleones (protones y neutrones), en interacción. Se refiere a la interacción que mantiene unidos a los quarks para formar hadrones, (protones, neutrones y mesones), por lo tanto permite mantener el núcleo unidos. Esta fuerza es la responsable de la estabilidad en toda la materia (Román). La partícula mediadora en esta interacción es el gluón. “Son fuerzas de corto alcance, actúan sólo a distancias que tienen las dimensiones del núcleo atómico”. (Zubero, 2010).

Interacción nuclear débil: Este tipo de fuerza es responsable de la desintegración beta de los núcleos de los átomos. Esta interacción es de corto alcance, es decir, distancias menores que las dimensiones del núcleo.
“Es la interacción responsable de que un quark de un tipo se transforme en un quark de otro tipo como ocurre en la desintegración Beta de los núcleos”. (Zubero, 2010). La partícula mediadora son los bosones.


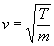









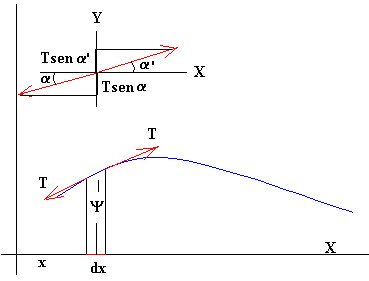
 (m es la densidad lineal de masa) situado en Q será:
(m es la densidad lineal de masa) situado en Q será:


 podemos escribir la potencia de una onda unidimensional como:
podemos escribir la potencia de una onda unidimensional como:
 ), para ello , basta que tengamos en cuenta que
), para ello , basta que tengamos en cuenta que  , de este modo la expresión que resulta es más general, puesto que será aplicable a todo tipo de ondas que se propaguen en dos o tres dimensiones.
, de este modo la expresión que resulta es más general, puesto que será aplicable a todo tipo de ondas que se propaguen en dos o tres dimensiones.
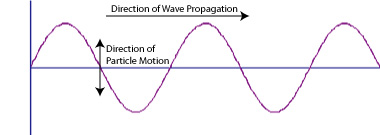
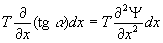

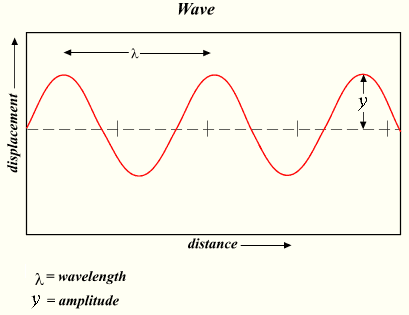
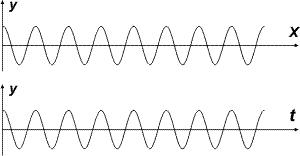
 "es la distancia entre dos crestas o valles seguidos. Se mide en unidades de longitud, tales como el metro(m), sus múltiplo o submúltiplos según convenga. Así, en la óptica, la longitud de onda de la luz se mide en nanómetros.
"es la distancia entre dos crestas o valles seguidos. Se mide en unidades de longitud, tales como el metro(m), sus múltiplo o submúltiplos según convenga. Así, en la óptica, la longitud de onda de la luz se mide en nanómetros.